I was asked by a student to demonstrate how to factorise 
This is taken from the Edexcel GCSE Maths Higher Student Book, which I recommend for its clear text and many worked problems.
Within this video, I’m trying to show how I ‘feel’ my way through factorising trickier expressions. It’s one of those things that come with practice!
Tangents Of A Parabola Problem
This is a problem from the excellent book ‘Pure Mathematics 2‘ by Backhouse, Houldsworth and Cooper, reviewed by Horril and originally published in 1963 although I’d recommend this and the companion volumes ‘Pure Mathematics 1‘ and ‘Applied Mathematics‘. All are well-explained, well-written books with many examples and practice questions.
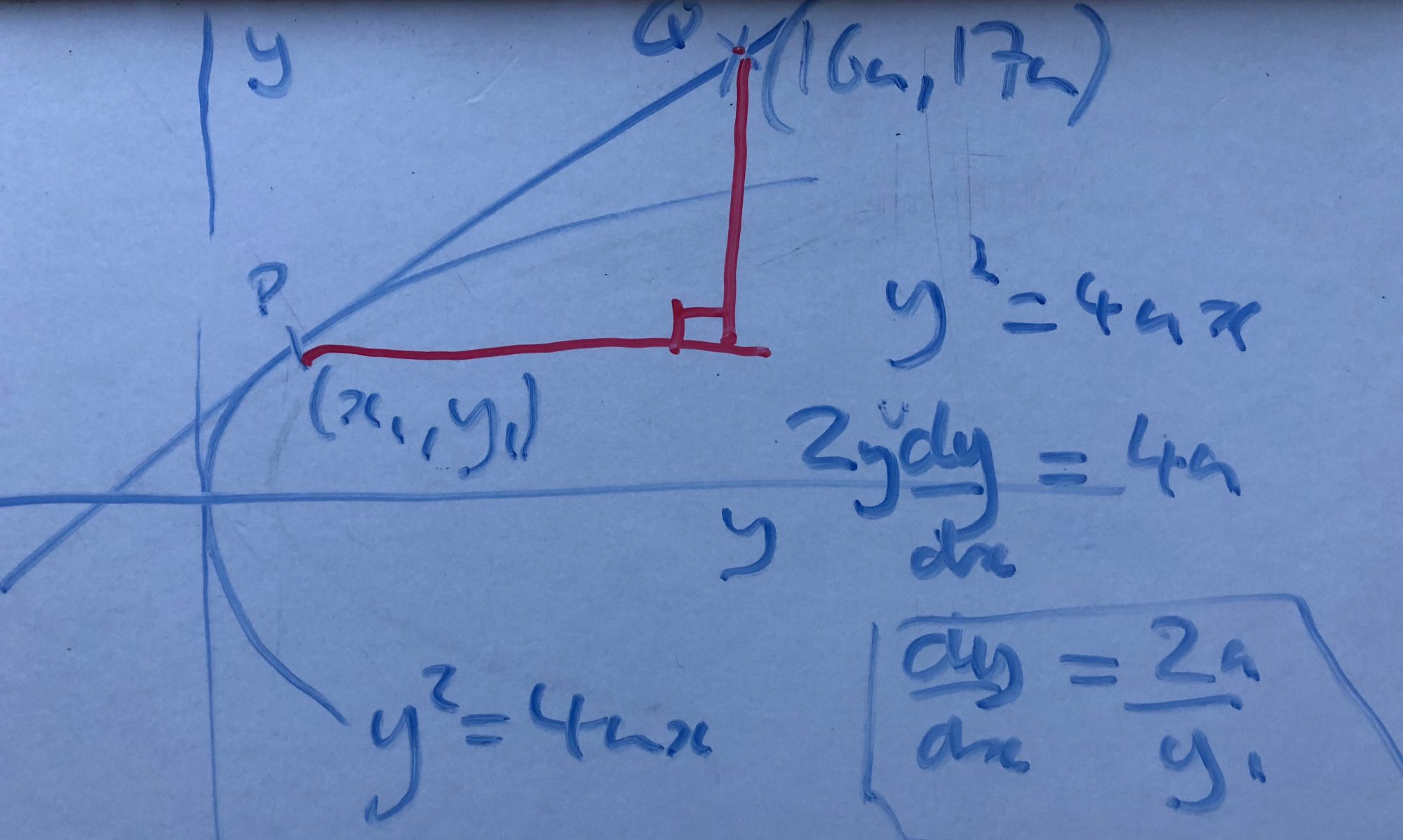
Within this video I demonstrate how to find the equation of the two tangents to the parabola 
from a point 
. To do this, we first define the problem in terms we can work with mathematically, our tangent on the parabola is defined as 
and we equate the gradient of the tangent to the parabola (derived in terms of 
through implicit differentiation) to the gradient of the line from .
from a point . To do this, we first define the problem in terms we can work with mathematically, our tangent on the parabola is defined as and we equate the gradient of the tangent to the parabola (derived in terms of through implicit differentiation) to the gradient of the line from .The resultant equation is simplified with a key substitution so resolves to a quadratic in terms of and 
, which is factorised to give two values of . These are substituted into to give the matching values of 
and then we use the values of and to derive the equations of both tangents to the parabola.
and , which is factorised to give two values of . These are substituted into to give the matching values of and then we use the values of and to derive the equations of both tangents to the parabola.I hope you enjoy, and please leave comments and requests!
